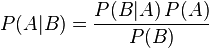贝叶斯定理是关于随机事件A和B的（或）的一則定理。

其中P(A|B)是在B发生的情况下A发生的可能性。

本博客所有内容是原创，如果转载请注明来源

 

先验概率与后验概率：假定B1,B2,……是某个过程的若干可能的前提，则P(Bi)是人们事先对各前提条件出现可能性大小的估计，称之为先验概率。如果这个过程得到了一个结果A，那么贝叶斯公式提供了我们根据A的出现而对前提条件做出新评价的方法。P(Bi∣A)既是对以A为前提下Bi的出现概率的重新认识，称 P(Bi∣A)为后验概率。在分类中求后验概率P(Ci | X)已知样本X，计算属于Ci类别的概率。X=(a1,a2...an)

朴素贝叶斯分类